logo slogan

Segger emLib CRC

 

emLib
The emLib CRC module allows checksum calculations of data using CRC, the Cyclic Redundancy Check. It is employed to provide an error-detection on data transfers in digital networks and storage devices. emLib CRC delivers generic CRC routines, allowing usage in more than one standard implementation at a time.
This page describes the CRC API functions and shows their usage based on example code.

 

What is CRC
Using emLib CRC
Core API functions
Performance and memory footprint
Example code
Sample applications

What is CRC?


The Cyclic Redundancy Check, short CRC, is an algorithm used for checksum calculations. The basic principle of CRC calculations was invented by W. Wesley Peterson in 1961, while many of today's standard implementations were published later on by several other researchers and mathematicians.

CRC is a cyclic block code used to calculate checksums, which themselves contain no information that was not already included in the raw data. Instead, the usefulness of CRC checksums originates from their inherent capacity to detect erroneous data in communication channels and storage devices, including any uneven number of bit errors and most two-bit errors, as well as any burst error of certain length. To do so, CRC algorithms require a generator polynomial that is used as a divisor in a polynomial division of the raw data for which to calculate the CRC. The remainder of this calculation is then considered the CRC checksum.

In hardware, CRC checksum calculations may be easily implemented using feedback shift-registers. The following example diagram illustrates the basic principle of these implementations:

 

 

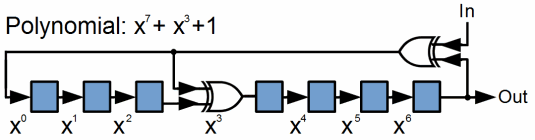
Generally, a CRC is called n-bit CRC if its checksum is n bits. Hence, for a given n, several different generator polynomials may be used to calculate several different n-bit CRCs. These generator polynomials have in common that they consist of n+1 terms (thus having a maximum degree of n) and that they are capable of detecting burst errors that affect n bits or less. Some CRCs are calculated using the most-significant-bit-first notation of polynomials, while others utilize the least-significant-bit-first notation of polynomials. Usage of different generator polynomials results in different error-detection properties, thus the selection of the proper generator polynomial is a question of vital importance. Some of the factors in this selection process are the length of the data for which to calculate the CRC, the desired error-detection properties, and the desired performance of the calculation.
Certain CRC calculation algorithms have been incorporated into technical standards that do not only define the generator polynomial to be used in the polynomial division, but also require compliance to further specifications such as initialization vectors.

 

Using emLib CRC


The emLib CRC module has a simple yet powerful API. It can be easily integrated into an existing application. The code is completely written in ANSI-C and is MISRA-C compliant.

To simply calculate a CRC for contiguous raw data, the application would only need to call one function. If two or more distinct data areas need to be processed into the same CRC, subsequent calls to the function may be used for incremental calculations over each of these areas.

emLib CRC does not offer API functions that are fully conformant to a specific standard implementation, but delivers generic CRC routines instead. This allows their usage in more than one standard implementation at a time, but requires the user to make sure initialization vectors and further specifications are performed from within the application.


All functionality can be verified with standard test patterns using the validation API functions. The functions for generating the lookup tables that are used for specific polynomials are also included for full transparency.

 

Core API functions


The table below lists the available emLib CRC API functions.

 

 

 Function

Description

SEGGER_CRC_Calc()

Table-driven implementation using arbitrary polynomials (LSB notation).

SEGGER_CRC_Calc_MSB()

Table-driven implementation using arbitrary polynomials (MSB notation).

SEGGER_CRC_Calc_BitByBit()

Bitwise implementation using arbitrary polynomials (LSB notation).

SEGGER_CRC_Calc_MSB_BitByBit()

Bitwise implementation using arbitrary polynomials (MSB notation).

SEGGER_CRC_Calc_48()

Table-driven implementation using the 7-bit polynomial 0x48 (LSB notation).

SEGGER_CRC_Calc_09()

Table-driven implementation using the 7-bit polynomial 0x09 (MSB notation).

SEGGER_CRC_Calc_8408()

Table-driven implementation using the 16-bit polynomial 0x8408 (LSB notation).

SEGGER_CRC_Calc_1021()

Table-driven implementation using the 16-bit polynomial 0x1021 (MSB notation).

SEGGER_CRC_Calc_82F63B78()

Table-driven implementation using the 32-bit polynomial 0x82F63B78 (LSB notation).

SEGGER_CRC_Calc_1EDC6F41()

Table-driven implementation using the 32-bit polynomial 0x1EDC6F41 (MSB notation).

SEGGER_CRC_Calc_EDB88320()

Table-driven implementation using the 32-bit polynomial 0xEDB88320 (LSB notation).

SEGGER_CRC_Calc_04C11DB7()

Table-driven implementation using the 32-bit polynomial 0x04C11DB7 (MSB notation).

SEGGER_CRC_Validate()

Function to validate the emLib CRC implementation.

 

 

Performance and memory footprint


The following table contains performance values for an emLib CRC release build as tested on a Cortex-M7 at 200 MHz, using the 32-bit polynomials 0xEDB88320 (LSB) and 0x04C11DB7 (MSB):

 

Implementation

Setup time
(cycles)

Cycles/byte

MByte/sec

Computation time
for 1 MByte of data

ROM usage

Bitwise, arbitrary polynomial (LSB)

-

124

1.53

650.12 ms

56 byte

Table‑driven, arbitrary polynomial (LSB)

784

17

11.21

89.13 ms

92 byte

Table‑driven, specified polynomial (LSB)

-

13

14.67

68.16 ms

1060 byte

Bitwise, arbitrary polynomial (MSB)

148

134

1.42

702.45 ms

168 byte

Table‑driven, arbitrary polynomial (MSB)

878

20

9.53

104.86 ms

234 byte

Table‑driven, specified polynomial (MSB)

-

11

17.33

57.67 ms

1056 byte

 

Example code


Using the 32-bit polynomial 0x04C11DB7 to verify the integrity of a message
This sample shows how to calculate a 32-bit CRC for a given message. Subsequently, it verifies the message's integrity by calculating the 32-bit CRC for the augmented message.

 

#include “SEGGER_CRC.h”

int main(void) {
  //
  // Declare variables.
  //
  U8  NumBytes;
  U8  SizeOfPoly;
  U32 Crc;
  U32 Poly;
  U32 InitialCRC;
  //
  // Sample message (8 bytes of data + 4 bytes for augmentation of 32-bit CRC).
  //
  U8  aMessage[12] = {
    0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC, 0x1C,
    0x0,  0x0,  0x0,  0x0
  };
  //
  // Init variables.
  //
  NumBytes   = 8;           // Number of bytes at aMessage.
  SizeOfPoly = 32;          // Size of the polynomial to use.
  Poly       = 0x04C11DB7;  // Arbitrary polynomial in MSB-first notation.
  InitialCRC = 0x1A2B3C4D;  // Initial value for incremental calculation.
  //
  // Calc CRC for given message.
  //
  Crc = SEGGER_CRC_CalcBitByBit_MSB(aMessage, NumBytes, InitialCRC, Poly, SizeOfPoly);
  //
  // Append resulting CRC to message.
  //
  aMessage[ 8] = (Crc >> 24) & 0xFF;
  aMessage[ 9] = (Crc >> 16) & 0xFF;
  aMessage[10] = (Crc >>  8) & 0xFF;
  aMessage[11] = (Crc >>  0) & 0xFF;
  //
  // Calc CRC for augmented message.
  // Non-zero result indicates erroneuos data.
  // Otherwise no error has been detected.
  //
  Crc = SEGGER_CRC_CalcBitByBit_MSB(aMessage, NumBytes + 4, InitialCRC, Poly, SizeOfPoly);
  if (Crc != 0) {
    return -1;
  } 
  return 0;
}

 

Sample applications


emLib includes sample applications to demonstrate its functionality and to provide an easy to use starting point for your application. The applications' source code is included in the shipment. The following applications are delivered with emLib CRC:

 

Application name

Target platform

Description

 CRCAugmentFile.exe

 Windows

Command line tool to augment a file with its calculated CRC. Uses the 32-bit polynomial 0x04C11DB7.

 CRCCalc.exe

 Windows

Command line tool to calculate the CRC for a given file using the bitwise API functions for arbitrary polynomials. Calculation parameters are configurable by the user.

 CRCValidate.exe

 Windows

Console application to validate the emLib CRC API using standard test patterns.

 CRCVerifyAugmentedFile.exe

 Windows

Command line tool to verify the integrity of an augmented file. Uses the 32-bit polynomial 0x04C11DB7.

 

 

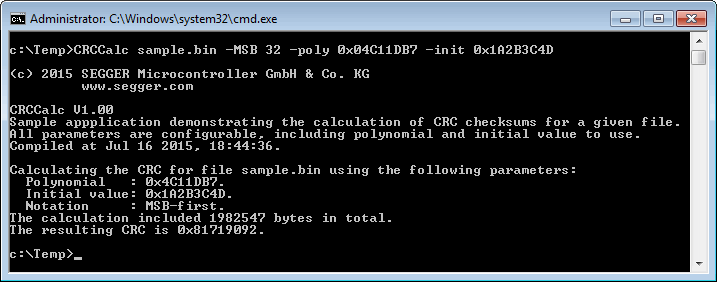
CRCAugmentFile


CRCAugmentFile is a Windows command line tool to augment a file with its calculated CRC. Typically, this is done by a sender before sending the file towards its recipient. CRCAugmentFile uses the 32-bit polynomial 0x04C11DB7 (MSB-first notation) and requires the file to not be write-protected. The application CRCVerifyAugmentedFile may be used to verify the augmented file's integrity.
Usage: CRCAugmentFile <sourcefile>

 

Parameter

Description

<sourcefile>

Path to the file for which to calculate the CRC. Must not be write-protected.

 

 

 

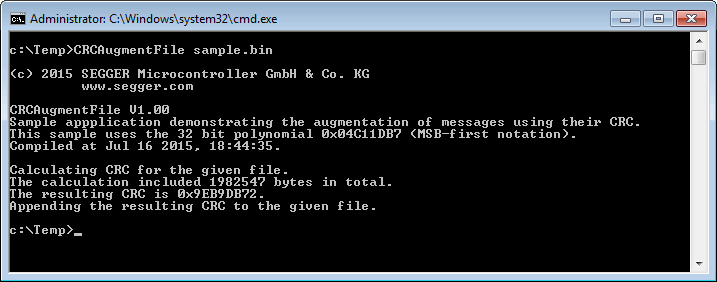
CRCCalc


CRCCalc is a Windows command line tool to calculate the CRC for a given file using the bitwise emLib CRC API functions for arbitrary polynomials. Further calculation parameters are configurable by the user, including the polynomial to use and an initial value for the calculation. CRCCalc may be used to easily calculate CRC checksums for arbitrary files.
Usage: CRCCalc <sourcefile> [-MSB [<SizeOfPoly>]] [-Poly <Polynomial>] [-init <InitialCRC>]

 

 

Parameter

Description

<sourcefile>

Path to the file for which to calculate the CRC..

[-MSB [<SizeOfPoly>]]

(Optional) Used to indicate MSB-first notation.
If not set, calculation is performed LSB-first.
If set and Polynomial is given, SizeOfPoly must indicate that polynomial's size.
If set and Polynomial is not given, a default polynomial of known size is used, hence SizeOfPoly is ignored and may be omitted.

[-poly <Polynomial>]

(Optional) Defines the polynomial to be used, which must not exceed a polynomial degree of 32. Expects hexadecimal notation.
If not set, the 16-bit polynomial 0x8408 is used for LSB-first calculations and the 16-bit polynomial 0x1021 is used for MSB-first calculations.

[-init <InitialCRC>]

(Optional) Initial value for incremental calculations. Expects hexadecimal notation.
If not set, 0x0 is used as initial value. 

 

 

CRCValidate


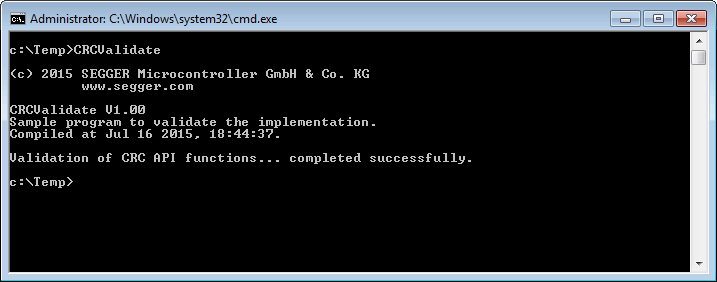
CRCValidate is a Windows console application to validate the emLib CRC API using standard test patterns. It uses the emLib CRC validation API to validate the implementation of the emLib CRC API functions. CRCValidate will display an error code if any validation fails, omitting further validation steps.

 

 

 

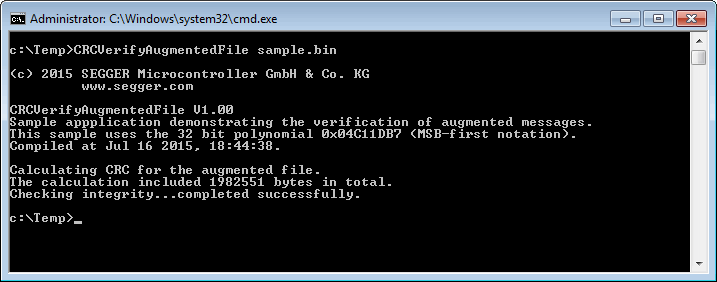
CRCVerifyAugmentedFile


CRCVerifyAugmentedFile is a Windows command line tool to verify the integrity of an augmented file. Typically, this is done by the file's recipient. CRCVerifyAugmentedFile uses the 32-bit polynomial 0x04C11DB7 (MSB-first notation). The application CRCAugmentFile may be used to augment a file with its calculated CRC.
Usage: CRCVerifyAugmentedFile <sourcefile>

 

Parameter

Description

<sourcefile>

Path to the file for which to calculate the CRC.